
Dạng 1 : khẳng định giao tuyến của nhì mặt phẳng () với ()
Phương pháp :
• Tìm nhì điểm chung tách biệt của nhì mặt phẳng () với ()
• Đường thẳng trải qua hai điểm thông thường ấy là giao tuyến phải tìm
Chú ý : Để tìm thông thường của () với () thường xuyên tìm 2 đường thẳng đồng phẳng lần lượt bên trong hai mp giao điểm nếu gồm của hai tuyến phố thẳng này là vấn đề chung của nhị mặt phẳng




Bạn vẫn xem đôi mươi trang chủng loại của tư liệu "Bài tập Hình học không gian lớp 11 tất cả lời giải", để cài đặt tài liệu cội về máy các bạn click vào nút DOWNLOAD sinh hoạt trên
BÀI TẬP HÌNH HỌC KHÔNG GIAN LỚP 11 CÓ LỜI GIẢIDạng 1 : xác minh giao tuyến của nhì mặt phẳng (a) cùng (b)Phương pháp : · Tìm hai điểm chung sáng tỏ của nhị mặt phẳng (a) và (b)· Đường thẳng trải qua hai điểm tầm thường ấy là giao tuyến đề xuất tìm để ý : Để tìm tầm thường của (a) và (b) hay tìm 2 con đường thẳng đồng phẳng lần lượt nằm trong hai mp giao điểm nếu bao gồm của hai tuyến đường thẳng này là điểm chung của nhì mặt phẳng
Bài tập : 1. Trong khía cạnh phẳng () đến tứ giác có các cặp cạnh đối không tuy nhiên song với điểm .a. Xác định giao đường của và (SBD)b. Khẳng định giao tuyến đường của (SAB) với (SCD)c. Xác định giao tuyến của (SAD) cùng (SBC)Giải a. Xác minh giao đường của (SAC) với (SBD)Ta bao gồm : S là điểm chung của (SAC) và (SBD)Trong (a), điện thoại tư vấn O = AC Ç BD · O Î AC mà AC Ì (SAC) Þ O Î (SAC) ·O Î BD mà lại BD Ì (SBD) Þ O Î (SBD) Þ O là điểm chung của (SAC) cùng (SBD) Vậy : SO là giao tuyến đường của (SAC) cùng (SBD) b. Xác định giao đường của (SAB) với (SCD)Ta có: S là vấn đề chung của (SAC) và (SBD)Trong (a) , AB không tuy nhiên song cùng với CDGọi I = AB Ç CD · I Î AB mà AB Ì (SAB) Þ I Î (SAB) · I Î CD nhưng CD Ì (SCD) Þ I Î (SCD)Þ I là vấn đề chung của (SAB) cùng (SCD)Vậy : mê mẩn là giao đường của (SAB) với (SCD)c. Tương tự câu a, b 2. Cho bốn điểm A,B,C,D không thuộc thuộc một khía cạnh phẳng .Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao để cho MN không song song cùng với BC. Tìm giao tuyến đường của (BCD) cùng (MNP) Giải · phường Î BD nhưng mà BD Ì (BCD) Þ p. Î (BCD) · p. Î (MNP)Þ P là vấn đề chung của (BCD) cùng (MNP) vào mp (ABC) , call E = MN Ç BC · E Î BC mà BC Ì (BCD) Þ E Î (BCD) · E Î MN mà lại MN Ì (MNP) Þ E Î (MNP) Þ E là điểm chung của (BCD) cùng (MNP)Vậy : PE là giao con đường của (BCD) và (MNP) 3. Cho tam giác ABC và một điểm S ko thuộc mp (ABC) , một điểm I ở trong đoạn SA .Một đường thẳng a không tuy nhiên song với AC cắt những cạnh AB, BC theo thiết bị tự tại J , K. Tìm kiếm giao tuyến của những cặp mp sau :a. Mp (I,a) với mp (SAC) b. Mp (I,a) với mp (SAB) c. Mp (I,a) và mp (SBC)Giảia. Kiếm tìm giao tuyến của mp (I,a) với mp (SAC) :Ta có:· IÎ SA mà SA Ì (SAC) Þ I Î (SAC)· IÎ(I,a)Þ I là vấn đề chung của hai mp (I,a) cùng (SAC ) trong (ABC), a không song song cùng với ACGọi O = a Ç AC · O Î AC cơ mà AC Ì (SAC) Þ O Î (SAC) · O Î (I,a) Þ O là điểm chung của hai mp (I,a) cùng (SAC) Vậy : IO là giao con đường của nhị mp (I,a) với (SAC) b. Tìm kiếm giao tuyến đường của mp (I,a) cùng với mp (SAB) : là JI c. Kiếm tìm giao đường của mp (I,a) với mp (SBC)Ta gồm : K là vấn đề chung của nhị mp (I,a) với mp (SBC) vào mp (SAC) , hotline L = IO Ç SC· L Î SC nhưng SC Ì (SBC) Þ L Î (SBC) · L Î IO mà lại IO Ì (I,a) Þ L Î (I,a) Þ L là điểm chung của nhị mp (I,a) với (SBC) Vậy: KL là giao tuyến của hai mp (I,a) cùng (SBC) 4.Cho tứ điểm A ,B ,C , D không cùng nằm trong một mpa. Chứng minh AB cùng CD chéo nhaub. Trên những đoạn trực tiếp AB và CD theo lần lượt lấy các điểm M, N làm sao để cho đường thẳng MN giảm đường trực tiếp BD tại I . Hỏi điểm I thuộc các mp nào .Xđ giao tuyến của hai mp (CMN) cùng (BCD)Giải a. Chứng minh AB cùng CD chéo cánh nhau :Giả sử AB cùng CD không chéo nhau cho nên vì vậy có mp (a) chứa AB với CDÞ A ,B ,C , D bên trong mp (a) mâu thuẩn giả thuyết Vậy : AB cùng CD chéo cánh nhaub. Điểm I thuộc đầy đủ mp : · I Î MN mà MN Ì (ABD) Þ I Î (ABD)· I Î MN mà lại MN Ì (CMN) Þ I Î (CMN)· I Î BD cơ mà BD Ì (BCD) Þ I Î (BCD) Xđ giao đường của hai mp (CMN) với (BCD) là CI5.Cho tam giác ABC phía bên trong mp (P) và a là mộtđường thẳng phía trong mp (P) với không song song với AB và AC . S là 1 điểm ở làm nên phẳng (P) với A’ là 1 điểm trực thuộc SA .Xđ giao tuyến của những cặp mp saua. Mp (A’,a) và (SAB)b. Mp (A’,a) với (SAC)c. Mp (A’,a) cùng (SBC) Giảia. Xđ giao đường của mp (A’,a) với (SAB)· A’ Î SA nhưng SA Ì (SAB) Þ A’Î (SAB) · A’ Î (A’,a) Þ A’ là vấn đề chung của (A’,a) và (SAB) vào (P) , ta có a không song song với AB gọi E = a Ç AB · E Î AB mà AB Ì (SAB) Þ E Î (SAB) · E Î (A’,a)Þ E là vấn đề chung của (A’,a) và (SAB)Vậy: A’E là giao tuyến của (A’,a) với (SAB)b. Xđ giao tuyến của mp (A’,a) cùng (SAC)· A’ Î SA mà SA Ì (SAC) Þ A’Î (SAC)· A’ Î (A’,a)Þ A’ là điểm chung của (A’,a) và (SAC) trong (P) , ta bao gồm a không tuy vậy song cùng với ACGọi F = a Ç AC· FÎ AC nhưng AC Ì (SAC) Þ F Î (SAC)· E Î (A’,a)Þ F là điểm chung của (A’,a) với (SAC)Vậy: A’F là giao con đường của (A’,a) với (SAC)c. Xđ giao tuyến của (A’,a) với (SBC)Trong (SAB) , điện thoại tư vấn M = SB Ç A’E· M Î SB mà lại SB Ì (SBC) Þ MÎ (SBC)· M Î A’E nhưng mà A’E Ì (A’,a) Þ MÎ (A’,a)Þ M là vấn đề chung của mp (A’,a) cùng (SBC) vào (SAC) , gọi N = SC Ç A’F· N Î SC cơ mà SC Ì (SBC) Þ NÎ (SBC)· N Î A’F cơ mà A’F Ì (A’,a) Þ NÎ (A’,a)Þ N là vấn đề chung của mp (A’,a) cùng (SBC) Vậy: MN là giao tuyến của (A’,a) và (SBC)6.Cho tứ diện ABCD , M là 1 trong điểm phía bên trong tam giác ABD , N là 1 trong những điểm bên trong tamgiác ACD . Kiếm tìm giao tuyến của những cặp mp saua. (AMN) cùng (BCD)b. (DMN) và (ABC)Giải a. Tìm kiếm giao đường của (AMN) và (BCD)Trong (ABD) , điện thoại tư vấn E = AM Ç BD· E Î AM mà lại AM Ì (AMN) Þ EÎ (AMN)· E Î BD nhưng BD Ì (BCD) Þ EÎ (BCD)Þ E là vấn đề chung của mp (AMN) và (BCD) vào (ACD) , gọi F = AN Ç CD· F Î AN mà lại AN Ì (AMN) Þ FÎ (AMN) · F Î CD nhưng mà CD Ì (BCD) Þ FÎ (BCD) Þ F là điểm chung của mp (AMN) với (BCD) Vậy: EF là giao đường của mp (AMN) và (BCD)b. Tìm giao tuyến đường của (DMN) cùng (ABC)Trong (ABD) , gọi p. = DM Ç AB· p Î DM nhưng mà DM Ì (DMN) Þ PÎ (DMN)· phường Î AB mà AB Ì (ABC) Þ PÎ (ABC)Þ P là vấn đề chung của mp (DMN) với (ABC) vào (ACD) , gọi Q = dn Ç AC· Q Î doanh nghiệp mà doanh nghiệp Ì (DMN) Þ QÎ (DMN)· Q Î AC mà AC Ì (ABC) Þ QÎ (ABCA)Þ Q là điểm chung của mp (DMN) và (ABC) Vậy: PQ là giao tuyến của mp (DMN) với (ABC)Dạng 2 : xác định giao điểm của mặt đường thẳng a với mặt phẳng (a) phương pháp : · Tìm đường thẳng b phía trong mặt phẳng (a)· Giao điểm của a cùng b là giao đt a với mặt phẳng (a) chăm chú : Đường trực tiếp b thường là giao tuyến đường của mp (a) cùng mp (b) É a
Cần chọn mp (b) đựng đường thẳng a sao cho giao tuyến của mp (a) cùng mp (b) dể xác minh và giao con đường không tuy nhiên song với đường thẳng a
Bài tập :1.Trong mp (a) mang đến tam giác ABC . Một điểm S không thuộc (a) . Trên cạnh AB rước một điểm p và trên các đoạn trực tiếp SA, SB ta đem lần lượt hai điểm M, N thế nào cho MN không tuy vậy song với AB .a. Tra cứu giao điểm của đường thẳng MN với phương diện phẳng (SPC)b. Search giao điểm của mặt đường thẳng MN với mặt phẳng (a)Giải a. Search giao điểm của đường thẳng MN với mặt phẳng (SPC)Cách 1 : trong (SAB) , call E = SP Ç MN · E Î SP mà SP Ì (SPC) Þ E Î(SPC)· E Î MNVậy : E = MN Ç (SPC) giải pháp 2 : · lựa chọn mp phụ (SAB) É MN· (SAB) Ç (SPC) = SP· vào (SAB), call E = MN Ç SPE Î MN E Î SP nhưng mà SP Ì (SPC) Vậy : E = MN Ç (SPC) b. Tìm giao điểm của con đường thẳng MN với mp (a) bí quyết 1: vào (SAB) , MN không tuy vậy song với ABGọi D = AB Ç MN· D Î AB nhưng mà AB Ì (a) Þ D Î(a) · D Î MNVậy: D = MN Ç (a)Cách 2 : · chọn mp phụ (SAB) É MN· (SAB) Ç (a) = AB· trong (SAB) , MN không tuy nhiên song cùng với ABGọi D = MN Ç ABD Î AB nhưng AB Ì (a) Þ D Î(a)D Î MNVậy : D = MN Ç (a)2. Mang lại tứ giác ABCD và một điểm S không thuộc mp (ABCD). Bên trên đoạn SC rước một điểm M không trùng cùng với S cùng C .Tìm giao điểm của con đường thẳng SD với mặt phẳng (ABM)Giải· chọn mp phụ (SBD) É SD· search giao đường của nhì mp (SBD) cùng (ABM) - Ta có B là điểm chung của (SBD) cùng (ABM)- tra cứu điểm phổ biến thứ hai của (SBD) và (ABM)Trong (ABCD) , hotline O = AC Ç BD vào (SAC) , gọi K = AM Ç SO KÎ SO nhưng SO Ì (SBD) Þ K Î(SBD)KÎ AM nhưng mà AM Ì (ABM) Þ K Î(ABM)Þ K là vấn đề chung của (SBD) cùng (ABM) Þ (SBD) Ç (ABM) = BK · trong (SBD) , điện thoại tư vấn N = SD Ç BK NÎ BK nhưng BK Ì (AMB) Þ N Î(ABM)N Î SDVậy : N = SD Ç (ABM)3. đến tứ giác ABCD cùng một điểm S không thuộc mp (ABCD). Bên trên đoạn AB mang một điểm M ,Trên đoạn SC lấy một điểm N (M , N không trùng với các đầu mút) . A. Tìm giao điểm của mặt đường thẳng AN với mặt phẳng (SBD) b. Tìm giao điểm của mặt đường thẳng MN với phương diện phẳng (SBD)Giảia. Search giao điểm của đường thẳng AN với mặt phẳng (SBD) · chọn mp phụ (SAC) É AN · tra cứu giao con đường của (SAC) và (SBD) trong (ABCD) , gọi p. = AC Ç BD Þ (SAC) Ç (SBD)= SP ·Trong (SAC), hotline I = AN Ç SP I Î AN I Î SP nhưng SP Ì (SBD) Þ I Î (SBD) Vậy : I = AN Ç (SBD)b. Tìm kiếm giao điểm của con đường thẳng MN với mặt phẳng (SBD)· chọn mp phụ (SMC) É MN· kiếm tìm giao con đường của (SMC) cùng (SBD)Trong (ABCD) , gọi Q = MC Ç BDÞ (SAC) Ç (SBD) = SQ·Trong (SMC), điện thoại tư vấn J = MN Ç SQJÎ MN J Î SQ nhưng SQ Ì (SBD) Þ J Î (SBD)Vậy: J = MN Ç (SBD)4. Cho 1 mặt phẳng (a) với một mặt đường thẳng m cắt mặt phẳng (a) trên C . Bên trên m ta đem hai điểm A, B và một điểm S trong không gian . Biết giao điểm của con đường thẳng SA với phương diện phẳng (a) là vấn đề A’ . Hãy xác định giao điểm của đường thẳng SB với mặt phẳng (a)Giải · chọn mp phụ (SA’C) É SB· kiếm tìm giao tuyến đường của (SA’C) và (a) Ta tất cả (SA’C) Ç (a) = A’C·Trong (SA’C), hotline B’ = SB Ç A’CB’Î SB mà SB Ì (SA’C) Þ B’ Î (SA’C) B’ Î A’C mà lại A’C Ì (a) Þ B’ Î (a) Vậy : B’= SB Ç (a) 5. Cho tư điểm A, B , C, S không thuộc ở vào một mặt phẳng . điện thoại tư vấn I, H theo lần lượt là trung điểm của SA, AB .Trên SC đem điểm K thế nào cho : ck = 3KS. Tìm giao điểm của mặt đường thẳng BC với phương diện phẳng (IHK)Giải· chọn mp phụ (ABC) É BC· tra cứu giao tuyến của (ABC) và (IHK)Trong (SAC) ,có IK không song song với ACGọi E’ = AC Ç IKÞ (ABC) Ç (IHK) = HE’·Trong (ABC), hotline E = BC Ç HE’E Î BC nhưng mà BC Ì (ABC) Þ E Î (ABC) E Î HE’ mà lại HE’ Ì (IHK) Þ E Î (IHK) Vậy: E = BC Ç (IHK)6. Mang đến tứ diện SABC .Gọi D là điểm trên SA , E là điểm trên SB với F là vấn đề trên AC (DE và ABkhông song song) .a. Xđ giao con đường của nhị mp (DEF) với (ABC)b. Kiếm tìm giao điểm của BC với mặt phẳng (DEF) c. Tra cứu giao điểm của SC với phương diện phẳng (DEF)Giải a. Xđ giao con đường của hai mp (DEF) với (ABC)Ta có : F là điểm chung của nhị mặt phẳng (ABC) với (DEF)Trong (SAB) , AB không song song cùng với DEGọi M = AB Ç DE · M Î AB cơ mà AB Ì (ABC) Þ M Î (ABC) · M Î DE nhưng mà DE Ì (DEF) Þ M Î (DEF)Þ M là điểm chung của hai mặt phẳng (ABC) cùng (DEF) Vậy: FM là giao đường của nhị mặt phẳng (ABC) cùng (DEF)b. Tra cứu giao điểm của BC với phương diện phẳng (DEF)· chọn mp phụ (ABC) É BC· tìm kiếm giao con đường của (ABC) với (DEF)Ta gồm (ABC) Ç (DEF) = FMhình 1·Trong (ABC), điện thoại tư vấn N = FM Ç BCNÎ BC N Î FM nhưng FM Ì (DEF) Þ N Î (DEF)Vậy: N = BC Ç (DEF)c. Tìm giao điểm của SC với phương diện phẳng (DEF)· chọn mp phụ (SBC) É SC· tìm kiếm giao đường của (SBC) với (DEF)Ta có: E là điểm chung của (SBC) với (DEF) N Î BC nhưng mà BC Ì (SBC) Þ N Î (SBC) N Î FM cơ mà FM Ì (DEF) Þ N Î (DEF)Þ N là vấn đề chung của (SBC) với (DEF)Ta có (SBC) Ç (DEF) = EN·Trong (SBC), call K = EN Ç SCKÎ SC K Î EN nhưng mà EN Ì (DEF) Þ K Î (DEF)hình 2Vậy: ... Ç BCÞI là điểm chung của (a) cùng (SAD)Ta có :Vậy : giao tuyến đường là mặt đường thẳng qua I và song song cùng với SA.5. Mang lại hình chóp S.ABCD gồm đáy ABCD là hình bình hành .Gọi M là một trong điểm trên cạnh SC và(a) là mặt phẳng cất AM và tuy vậy song với BD.a.Hãy nêu biện pháp dựng những giao điểm E, F của khía cạnh phẳng (a) thứu tự với các cạnh SB, SD.b. Call I là giao điểm của ME và CB , J là giao điểm của MF với CD. Hãy minh chứng ba điểm I,J, A thẳng hàng .Giảia.Hãy nêu giải pháp dựng những giao điểm E, F của khía cạnh phẳng (a) thứu tự với các cạnh SB, SD.Giả sử dựng được E, F thỏa vấn đề Ta bao gồm : Do những điểm E ,F ,A ,M thuộc thuộc mặt phẳng (a) trong (a) , gọi
K = EF Ç AM ·K Î EF mà lại EF Ì (SBD)Þ K Î (SBD)·K Î AM cơ mà AM Ì (SAC)Þ K Î (SAC)Þ K Î (SAC) Ç (SBD)Do (SAC) Ç (SBD) = SOÞK Î SO phương pháp dựng E, F :Dựng giao điểm K của AM và SO , qua K dựng EF // BDb.Chứng minh bố điểm I , J , A thẳng hàng :Ta bao gồm : ÞI Î (a) Ç (ABCD)Tương tự , ÞI , J , A là vấn đề chung của (a) cùng (ABCD)Vậy : I , J , A thẳng sản phẩm .6.Trong mặt phẳng (a) đến tam giác ABC vuông tại A , = 60, AB = a .Gọi O là trung điểm của BC . Rước điểm S ở những thiết kế phẳng (a) thế nào cho SB = a với SB ^ OA . điện thoại tư vấn M là mối điểm bên trên cạnh AB , phương diện phẳng (b) qua M song song cùng với SB với OA , giảm BC ,SC , SA thứu tự tại N , phường , Q .Đặt x = BM (0
Trong công tác môn Toán cung cấp THPT, phân môn Hình học không khí được nghiên cứu chủ yếu ớt trong công tác Hình học lớp 11 với cấu tạo gồm 2 chương: "Chương II. Đường thẳng với mặt phẳng trong không gian. Quan liêu hệ tuy nhiên song và Chương III. Tình dục vuông góc". Ngôn từ của Chương II được sách giáo khoa trình bày với kỹ năng và kiến thức hàn lâm, đa số là lí thuyết và bài bác tập lí thuyết, định tính, phần đông không gồm ví dụ hoặc bài xích tập nào làm cho học sinh có cơ hội hình thành cùng phát triển năng lượng tính toán. Những tài liệu với sách tìm hiểu thêm về Hình học không gian dành cho cấp thpt mà tôi biết khi viết về Chương II này cũng phần đông rất không nhiều hoặc không có các bài xích tập bao gồm nội dung để học sinh có thời cơ phát triển năng lượng tính toán. Qua thực tiễn giảng dạy nhiều năm trên trường thpt Triệu đánh 3, tôi nhận biết rằng hầu hết giáo viên với học sinh của nhà trường không có hứng thú khi dạy với học chương này vị lí bởi vì như đã trình bày ở trên. Điều này dần dẫn mang lại một yếu tố hoàn cảnh là nhiều học sinh ở trong nhà trường cho rằng môn Hình học không gian là một môn học khó, nhiều định nghĩa, định lí, hệ quả nặng nề nhớ và bài xích tập thì chẳng gồm gì thú vị. Thậm chí là trong một vài năm học trước đây, gồm có em học viên được review là học tập sinh giỏi toán (được chọn trong đội tuyển 5 em tham dự cuộc thi HSG Toán lớp 12 cấp cho tỉnh) nhưng mà vẫn thấy "ngại" khi giải quyết các việc về Hình học không gian.
Cũng tự việc thâu tóm được trung tâm lí của những em học viên khi bắt đầu tiếp cận với phân môn Hình học không khí này, trong quy trình dạy học, tôi đang "chế biến, thêm gia giảm" vào các bài tập vào sách giáo khoa và một số sách bài xích tập hình học không gian khác, mà tập trung chủ yếu vào những bài tập về dựng thiết diện để sở hữu được một hệ thống các bài bác tập về thiết diện và ăn diện tích của thiết diện giao hàng cho mục đích dạy học tập theo triết lý hình thành và phát triển các năng lực Toán học tập của học sinh; tạo cho các em chổ chính giữa lí hứng thú, say mê và thích thăm khám phá, tìm tòi khi học tập cỗ môn Hình học không gian ngay từ bài học kinh nghiệm đầu tiên, góp phần nâng cao chất lượng dạy học cỗ môn Toán nói chung tương tự như phân môn Hình học không gian lớp 11 dành riêng ở trường thpt Triệu đánh 3 trong các năm học sát đây.
cùng với những kết quả đạt được những bước đầu tiên như trên, tôi đã ra quyết định chọn đề tài: Thiết kế một trong những bài tập về thiết diện trong "Chương II. Đường thẳng cùng mặt phẳng trong không gian. Quan tiền hệ tuy vậy song - Hình học 11" theo lý thuyết phát triển các năng lực Toán học tập của học viên góp phần cải thiện chất lượng dạy dỗ học phân môn Hình học không khí ở trường trung học phổ thông Triệu sơn 3 làm đề tài sáng tạo độc đáo kinh nghiệm của phiên bản thân trong thời điểm học 2015-2016 với hy vọng được các đồng nghiệp trong với ngoài đơn vị đóng góp ý kiến, dìm xét và reviews để vấn đề được hoàn thành hơn.
1.2. Mục đích nghiên cứu
Mục đích nghiên cứu của đề bài là kiến thiết một khối hệ thống các bài tập về thiết diện và ăn diện tích của tiết diện trong Chương II. Đường thẳng với mặt phẳng trong không gian. Quan liêu hệ tuy vậy song - Hình học 11 nhằm định hướng hình thành và trở nên tân tiến cho học sinh những năng lực, kĩ năng sau đây:
- năng lực tư duy, năng lực tính toán.
- năng lực vận dụng các kiến thức về Hệ thức lượng giác trong công tác Hình học tập lớp 10 vào các bài toán Hình học không gian lớp 11 mà hầu hết là Định lí Côsin, phương pháp tính độ dài con đường trung tuyến đường và những công thức tính diện tích s tam giác.
- cách tân và phát triển trí tưởng tượng không gian, khả năng biểu diễn hình không gian.
- năng lượng sử dụng các công cụ, phương tiện cung ứng tính toán mà cụ thể ở đây là năng lực sử dụng những loại máy tính xách tay cầm tay.
- năng lực sử dụng ngôn từ Toán học.
1.3. Đối tượng nghiên cứu và phân tích
- Đối tượng nghiên cứu và phân tích của chủ đề là hệ thống các bài xích tập về thiết diện và diện tích của tiết diện trong Chương II - Hình học không khí lớp 11 được thiết kế theo lý thuyết phát triển các năng lực Toán học của học tập sinh, qua đó xác định sự cần thiết phải xây dựng khối hệ thống bài tập này trong chương trình giảng dạy phân môn Hình học không gian lớp 11.
1.4. Cách thức nghiên cứu giúp
phương pháp nghiên cứu thực hiện trong đề tài bao gồm:
- cách thức điều tra điều tra thực tế, tích lũy thông tin: Điều tra, khảo sát thực tế dạy học toán nói thông thường và dạy dỗ học phân môn Hình học không khí ở trường trung học phổ thông Triệu tô 3 nhằm từ kia thấy được tầm đặc trưng của vấn đề xây dựng hệ thống bài tập về tiết diện trong Chương II - Hình học không gian lớp 11 vào việc nâng cấp chất lượng dạy dỗ học .
- phương thức nghiên cứu giúp xây dựng các đại lý lý thuyết: Trên các đại lý tài liệu triển lẵm chương trình môn học, chuẩn chỉnh kiến thức - kỹ năng, sách giáo khoa Hình học tập 11 - nâng cấp và tài liệu về dạy học theo triết lý phát triển năng lực học sinh để xây dựng hệ thống bài tập theo mục đích đã đặt ra.
2. NỘI DUNG SÁNG KIẾN ghê NGHIỆM
2.1. Cơ sở lí luận của ý tưởng kinh nghiệm
Nghị quyết họp báo hội nghị BCH tw Đảng lần vật dụng tám (Khóa XI) về đổi mới căn bản, toàn diện giáo dục và huấn luyện và đào tạo nêu rõ: "Tiếp tục đổi mới mạnh mẽ phương thức dạy cùng học theo phía hiện đại; phát huy tính tích cực, công ty động, trí tuệ sáng tạo và áp dụng kiến thức, tài năng của người học; khắc phục và hạn chế lối truyền dạy áp đặt một chiều, ghi nhớ sản phẩm móc. Tập trung dạy giải pháp học, biện pháp nghĩ, khích lệ tự học, tạo cửa hàng để tín đồ học tự update và thay đổi tri thức, kỹ năng, cải tiến và phát triển năng lực...."
Mọi bạn đều cần được học toán và cần sử dụng toán trong cuộc sống đời thường hàng ngày. Chính vì như thế mà Toán học gồm vị trí đặc trưng đối với toàn bộ các nghành trong cuộc sống xã hội. đọc biết về Toán học giúp cho người ta có thể tính toán, suy nghĩ, ước lượng,...và nhất là có được phương thức tư duy, cách thức suy nghĩ, suy luận lôgic,...trong xử lý các sự việc nảy sinh, trong học tập tập cũng như trong cuộc sống thường ngày hàng ngày.
Ở trường phổ thông, học tập toán về cơ phiên bản là vận động giải toán. Giải toán liên quan đến việc lựa chọn và áp dụng đúng đắn các kiến thức, khả năng cơ bản, mày mò về các con số, sản xuất mô hình, giải thích số liệu, điều đình các ý tưởng phát minh liên quan,... Giải toán yên cầu phải tất cả tính sáng sủa tạo, hệ thống. Học toán và giải toán giúp học sinh tự tin, kiên nhẫn, bền bỉ, biết làm việc có phương pháp. Kỹ năng và kiến thức môn Toán còn được ứng dụng, giao hàng cho vấn đề học các môn học khác như Vật lí, Hóa học, Sinh học,...
bởi vì đó, sinh sống trường thêm nói chung, vấn đề dạy học tập môn Toán để đáp ứng được yêu thương cầu đổi mới trong giai đoạn bây giờ phải tập trung vào vấn đề hình thành và phát triển các năng lượng chung cũng tương tự các năng lực chuyên biệt của môn Toán như: năng lực tư duy (gồm: tư duy lôgic; bốn duy phê phán; bốn duy sáng sủa tạo; kĩ năng suy diễn, lập luận toán học), Năng lực tính toán (gồm: năng lực sử dụng những phép tính; năng lượng sử dụng ngôn ngữ toán; năng lực quy mô hóa; năng lượng sử dụng công cụ, phương tiện cung cấp tính toán). Cải tiến và phát triển trí tưởng tượng không gian, trực giác Toán học.
2.2. Hoàn cảnh của vấn đề trước lúc áp dụng sáng kiến kinh nghiệm
Trường thpt Triệu tô 3 được thành lập năm 1979 trên cơ sở tách bóc ra thành phân hiệu từ trường thpt Triệu sơn 1 và cho năm 1984 đồng ý mang tên như bây giờ. Là ngôi trường nằm tại vị trí phía Tây của huyện Triệu Sơn, trong vùng bao gồm điều kiện tài chính khó khăn độc nhất của thị trấn Triệu tô với địa bàn tuyển sinh có đến 4/8 làng mạc thuộc khoanh vùng miền núi với vùng đặc biệt khó khăn V134, V135; số học sinh là con em các dân tộc ít người chiếm gần 15%, số học sinh thuộc diện được nhà nước hỗ trợ chi phí học tập, được miễn giảm ngân sách học phí trong năm học tập 2015-2016 là 604 em, sở hữu tới 2/3 số học viên toàn trường. Chất lượng tuyển sinh đầu vào cũng rất thấp, cùng với điểm chuẩn đầu vào trung bình khoảng tầm từ 3,5 đến 4,0 điểm/môn.
với điều kiện như thế thì từ những năm 2005 quay trở lại trước, unique giáo dục mũi nhọn của nhà trường xét bên trên hai tiêu chí là công dụng thi HSG cấp cho tỉnh và tác dụng thi đh còn tương đối thấp. Từ năm học 1999- 2000 cho năm học 2004- 2005 chỉ bao gồm 6 giải HSG cung cấp tỉnh môn Toán (cao độc nhất vô nhị là giải Ba), thậm chí là năm học tập 2004-2005 nhà trường còn "trắng bảng" HSG so với 4 môn thoải mái và tự nhiên Toán, vật dụng lí, Hóa học và Sinh học. Số lượng học viên đậu đại học trong những năm trường đoản cú 1999 cho 2005 chỉ tầm vài chục em từng năm với đều ở mức điểm đa số là 15 đến 22 điểm.
lúc được cắt cử về công tác tại trường từ thời điểm tháng 8 năm 2004 với đảm nhận đào tạo môn Toán mặt khác là GVCN lớp "mũi nhọn số 1" của nhà trường với nhiệm vụ được giao khi hoàn thành khóa học tập là lớp buộc phải có ít nhất 5 giải HSG cấp tỉnh môn Toán (thời kỳ đó mỗi nhóm tuyển HSG văn hóa truyền thống có tối đa 10 em) cùng có ít nhất 30 em đỗ ĐH, tôi vẫn trăn trở khôn xiết nhiều. Cũng từ đa số trăn trở đó, trong quy trình dạy học, tôi sẽ không dứt tìm tòi, kiến thiết và biên soạn nhiều siêng đề dạy học cùng với nội dung tập trung vào việc phát triển các năng lực tư duy toán học với rèn luyện các khả năng giải toán cho học viên (thực tế khi ngừng khóa học 2004-2007, tôi đạt được chỉ tiêu đưa ra với 5 giải HSG văn hóa truyền thống cấp tỉnh giấc môn Toán, trong các số đó có 01 giải nhị môn Toán đầu tiên ở trong nhà trường; lớp có 31 em đỗ ĐH, trong các số ấy có 01 em đạt 27,5 điểm trường ĐH Bách Khoa HN, nhiều em lấy điểm trên 25,0; tất cả 01 em ăn điểm 10 môn Toán, 01 em đạt 9,5 điểm môn Toán và những em ăn điểm Toán từ 9,0 trở lên). Trong những chuyên đề đó, tôi rất trọng điểm đắc với chuyên đề: một số trong những bài tập về tính diện tích của tiết diện trong "Chương II. Đường thẳng với mặt phẳng trong ko gian. Quan hệ tuy vậy song - Hình học tập 11" bởi nguyên nhân kiểu bài xích tập này phần đông rất ít xuất hiện thêm trong SGK tương tự như trong các tài liệu xem thêm về Hình học tập không gian, không chỉ có vậy khi học chuyên đề này, học viên rất hứng thú với kỹ năng đo lường các đại lượng hình học của học viên được nâng lên ngay từ những bài bác học đầu tiên có đặc thù “nhập môn” Hình học tập không gian, qua đó các em khôn cùng tự tin khi tham gia học môn Hình học không khí - một môn học mà không phải học sinh nào đều thích (kể cả học viên khá, giỏi).
2.3. Những sáng kiến kinh nghiệm tay nghề đã thực hiện để xử lý vấn đề
2.3.1. Xây cất các bài bác tập về thiết diện trong “§1. Đại cương cứng về con đường thẳng và mặt phẳng”
tức thì từ bài học đầu tiên có tính chất “nhập môn” Hình học không gian này, tôi đã thi công và cung cấp cho học viên một số bài xích tập về dựng thiết diện và tính diện tích của tiết diện để học viên rèn luyện kỹ năng vẽ hình và màn trình diễn hình ko gian, hiện ra và cải cách và phát triển ở học sinh năng lực tư duy, năng lực giám sát thông qua bài toán đi đo lường và thống kê các đại lượng hình học như độ dài đoạn thẳng, diện tích của đa giác,..
Dưới đó là một số bài xích tập của phần này mà tôi đã kiến thiết và tổ chức dạy học tập ở đơn vị chức năng công tác:
Bài 1.1.
Bạn đang xem: Bài tập hình học không gian lớp 11 theo chủ đề
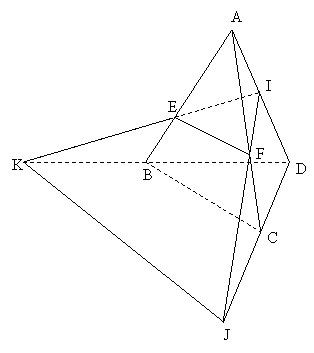
mang lại tứ diện ABCD. Gọi I là trung điểm của AD; J là vấn đề đối xứng cùng với D qua C; K là điểm đối xứng cùng với D qua B. Xác định thiết diện của tứ diện với khía cạnh phẳng (IJK).
Phân tích: (Hình 1.1)
- Đây là dạng bài tập cơ bạn dạng trong SGK. Học tập sinh thuận lợi xác định được tiết diện là tam giác IEF.
| - trường hợp chỉ dừng lại ở bài toán dựng tiết diện thì đấy là bài toán khá đơn giản dễ dàng đối với học viên và thông thường các học sinh có học tập lực trường đoản cú trung bình khá trở lên không tồn tại hứng thú lắm với bài tập này. - Để rèn luyện tài năng sử dụng những hệ thức lượng trong tam giác và năng lực tính toán, chế tác thêm hứng thú học tập tập mang đến học sinh, ta bổ sung cập nhật thêm mang thiết vào cho việc và thêm trách nhiệm cho học viên như sau: “Hãy tính diện tích của thiết diện lúc biết độ dài toàn bộ các cạnh của tứ diện bằng a ?” |
 |
- Đứng trước yêu cầu này, học sinh phải đi tìm cách tính diện tích tam giác IEF. Ta rất có thể vạch ra cho học sinh một số hướng lưu ý đến như sau:
1. Hãy đi tìm cách tính độ dài các cạnh của tam giác IEF.
- Tính được
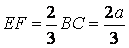
- Áp dụng Định lí Côsin vào tam giác AIE và AIF hoàn toàn có thể tính được
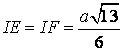
2. Để tính diện tích tam IEF có thể lựa chọn cách dựng mặt đường cao trường đoản cú đỉnh I và áp dụng Định lí Pitago để tính độ dài con đường cao, hoặc hoàn toàn có thể sử dụng trực tiếp phương pháp Hêrông
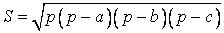
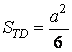
dấn xét 1.1:
1. Khi thi công bài tập theo phía ở trên trong quá trình dạy học Chương II- HHKG lớp 11, tôi nhận biết có một số công dụng rõ rệt như sau:
trang bị nhất, những tiết dạy học HHKG đa dạng mẫu mã và phong phú và đa dạng hơn, học viên có hứng thú rộng trong quy trình học tập cỗ môn HHKG.
thứ hai, học viên có cơ hội phát triển một số trong những năng lực cũng tương tự rèn luyện những kỹ năng quan trọng trong môn Toán làm việc cấp trung học phổ thông như: năng lực tính toán, kĩ năng vận dụng linh hoạt các Hệ thức lượng trong tam giác ở lịch trình Hình học tập lớp 10 vào phần HHKG lớp 11, kĩ năng biễu diễn hình không gian,…
vật dụng ba, tôi thiết suy nghĩ trong quá trình dạy học, so với người thầy, việc thiết kế các bài tập như kiểu bài 1.1 là rất phải thiết, duy nhất là ở một trong những nội dung dạy dỗ học, chẳng hạn như ở Chương II – HHKG lớp 11, khi những bài tập trong SKG và trong những tài liệu tìm hiểu thêm có cực kỳ ít bài xích tập (thậm chí là không có) làm cho học sinh có cơ hội phát triển các năng lực Toán học cũng như rèn luyện các kĩ năng đã nói ngơi nghỉ trên.
2. Bao gồm nhiều cách để tính diện tích s một tam giác, tuy nhiên khi dạy môn HHKG, tôi thường kim chỉ nan cho học sinh sử dụng công thức Hêrông để tính vày lẽ bí quyết này được trình diễn trong SGK Hình học tập 10, hơn thế nữa khi học sinh có sự cung ứng tính toán của các loại máy vi tính cầm tay mới bây chừ thì câu hỏi tính diện tích s tam giác sẽ rất nhanh.
3. Tùy theo mức độ kiến thức của học viên mà trong quy trình hướng dẫn học sinh học tập, ta có thể nhắc lại một số trong những hệ thức lượng trong tam giác cho những em ôn tập lại với ghi lưu giữ sâu hơn.
4. Để gồm thêm nội dung luyện tập cho học sinh, ta có thể đổi khác tính hóa học của tứ diện, chẳng hạn, mang đến giả thiết cụ đổi:
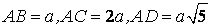

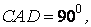
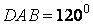
bài bác 1.2. Cho hình chóp SABCD gồm đáy là hình vuông vắn cạnh bởi , các cạnh bên bằng nhau và bằng
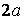
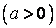
Phân tích: (Hình 1.2)
- rất có thể xác định được thiết diện là ngũ giác MKNPQ.
- Để tính diện tích s thiết diện, có thể định phía cho học sinh theo 2 biện pháp sau:
cách 1:
- sử dụng Định lí Côsin mang đến tam giác SAB để tính
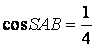
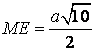
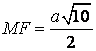
- thực hiện Định lí Pitago nhằm suy ra
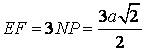
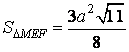
- minh chứng
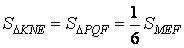
- Từ kia suy ra
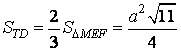
| biện pháp 2: - rất có thể chia việc tính diện tích thiết diện thành vấn đề tính diện tích tam giác MKQ và hình thang KNPQ. - bằng cách tính độ lâu năm 3 cạnh của tam giác MKQ theo định lí Côsin và sau đó áp dụng công thức Hêrông để tính diện tích tam giác này. - Tính các cạnh của hình thang KNPQ, thấy được đó là hình thang cân, từ này cũng tính được diện tích hình thang. |
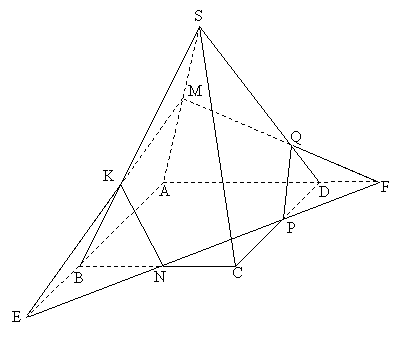 |
Nhận xét 1.2:
1. Việc xuất vạc của bài bác 1.2 nghỉ ngơi trong SGK chỉ yêu cầu khẳng định thiết diện với giả thiết hình chóp bao gồm đáy là hình bình hành. Việc không ngừng mở rộng và thiết kế thành bài bác 1.2 đã giúp cho ta bao gồm thêm các phương án để rèn luyện các kỹ năng cần thiết trong môn Toán nói tầm thường và môn HHKG nói riêng mang đến học sinh.
2. Thông qua việc đào bới tìm kiếm tòi và lời khuyên các phương án tính diện tích s thiết diện đã tạo nên và phát triển ở học sinh mức độ tư duy cao hơn, trở nên tân tiến tối đa các năng lực Toán học của học sinh, nhất là các học viên có học lực từ bỏ trung bình tương đối trở lên.
3. Trong vượt trình xây đắp và tổ chức triển khai học rượu cồn dạy học các bài tập như trên, họ chỉ nên triết lý cho học viên tìm tòi lời giải, còn câu hỏi tính toán, trình bày lời giải ví dụ là của học sinh. Ta buộc phải đưa ra yêu thương cầu khác biệt tùy theo mức độ nhấn thức của từng học tập sinh, chẳng hạn so với các học sinh có học tập lực trung bình hơi trở xuống chỉ nên yêu mong tính độ dài của một cạnh nào đó; còn so với học sinh khá, xuất sắc thì yêu thương cầu cấu hình thiết lập công thức tính diện tích s ở vô số cách khác nhau,…
bài 1.3. Cho hình lập phương ABCD.A"B"C"D" cạnh bởi . Call M, N thứu tự trung điểm của AB, AD. Hãy dựng thiết diện của hình phương với khía cạnh phẳng (C"MN) và tính diện tích s của thiết diện đó theo .
| Phân tích: (Hình 1.3) - thiết diện là ngũ giác C’INMJ. - có thể hướng dẫn cho học sinh tính diện tích s của tiết diện này giống như theo cách của bài bác 1.2. - cụ thể: Tính được 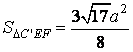 Chứng minh được
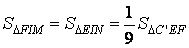 Từ đó có 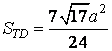 |
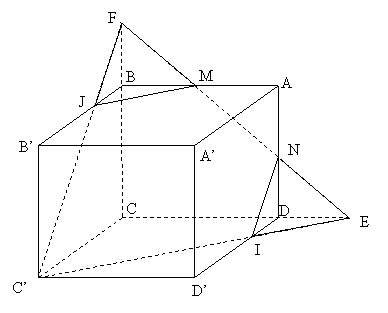 |
bài xích 1.4. Cho tứ diện đều ABCD có cạnh bằng . Hotline M là trung điểm của AB; E là điểm thuộc mặt đường thẳng BC thế nào cho C là trung điểm của BE. Xác minh thiết diện của tứ diện với khía cạnh phẳng (DME) cùng tính diện tích s của thiết diện này theo .
| Phân tích: (Hình 1.4) - thiết diện là tam giác DMN. - sử dụng định lí Côsin tính được những cạnh:
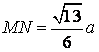 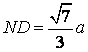 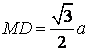 |
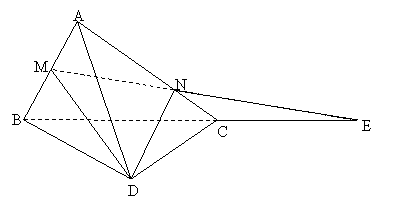 |
- áp dụng công thức Hêrông hoàn toàn có thể tính được:
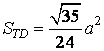
bài bác 1.5. Cho tứ diện đa số ABCD tất cả cạnh bởi . điện thoại tư vấn M và N thứu tự là trung điểm của AB với BC, P là điểm trên cạnh CD làm thế nào để cho CP = 2PD.
a) Dựng tiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Thiết diện là hình gì?
b) Tính diện tích s thiết diện theo .
| Phân tích: (Hình 1.5) - thiết diện là tứ giác MNPQ. - có thể minh chứng được AQ = 2QD, từ kia suy ra tiết diện là hình thang cân. - áp dụng định lí Côsin tính được những cạnh MQ với NP của hình thang, sau đó tính được đường cao chính phủ quốc hội của hình thang.
|
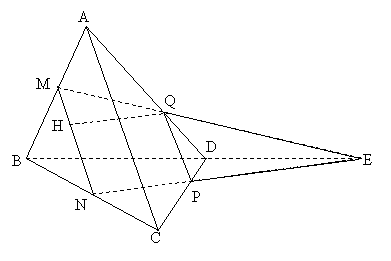 |
- Từ đó tính được diện tích s thiết diện là:
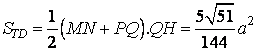
Nhận xét 1.3:
1. Bài bác “§1. Đại cương về mặt đường thẳng cùng mặt phẳng” thông thường được dạy dỗ trong từ 2-3 tiết lý thuyết và 1-2 tiết thắc mắc & bài bác tập. Trong các 16 câu hỏi và bài xích tập (SGK Hình học 11-NC), chỉ tất cả 2 bài tương quan đến việc khẳng định thiết diện. Qua thực tiễn nhiều năm dạy dỗ học tôi thấy rằng, giả dụ chỉ dựng chân lại tại việc xử lý các thắc mắc và bài xích tập trong SGK cơ mà không kiến tạo hoặc mở rộng hơn, thì các tiết học (kể cả kim chỉ nan và bài bác tập) sẽ khá tẻ nhạt và không khiến được hứng thú học tập mang lại học sinh, độc nhất là học sinh các lớp trực thuộc Ban KHTN.
2. Thực tiễn cho thấy, cùng với việc kiến tạo thêm các bài tập tất cả nội dung định lượng như trên, những tiết học tập HHKG đã diễn ra sôi nổi ngay từ các tiết học tập đầu tiên; học sinh không hầu hết có thời cơ được cải cách và phát triển năng lực đo lường của phiên bản thân mà hơn nữa có cơ hội để ôn tập lại và vận dụng những kiến thức về Hệ thức lượng trong tam giác ở chương trình Hình học 10 vào xử lý các sự việc của HHKG lớp 11; các học sinh khá, xuất sắc có cơ hội để khuyến cáo nhiều phương án khác nhau trong việc tính diện tích s một nhiều giác. Điều này rất có ích khi những em học cho phần tính khoảng cách từ điểm đến mặt phẳng, các em sẽ áp dụng rất thành thạo phương pháp tính khoảng cách theo cách thức thể tích
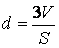
3. Việc xây dựng các bài tập như trên hoàn toàn theo hướng “mở”, tức là tùy theo năng lực của từng đối tượng học sinh mà bạn giáo viên nên biến hóa các trả thiết cho phù hợp. Chẳng hạn đối với nhóm học viên trung bình hơi hoặc khá thì nên cần cho giả thiết là tứ diện hồ hết (các bài 1.1, 1.4, 1.5); còn đối với nhóm học sinh xuất sắc thì nên cho mang thiết về tứ diện cùng với độ dài những cạnh khác nhau, đòi hỏi các em trong quy trình đi tính diện tích s thiết diện phải áp dụng thật linh động định lí Côsin trong vô số nhiều tam giác khác nhau.
4. Trong quá trình dạy học tập môn HHKG, việc hình thành ở học viên kỹ năng vẽ hình (biễu diễn hình ko gian) cũng rất quan trọng. Có thể khẳng định việc có một hình biểu diễn xuất sắc là trong những yếu tố ra quyết định để hình thành lời giải bài tập. Để làm tốt điều này, người giáo viên cần định hướng cho học viên biểu diễn các hình không khí dưới những “góc nhìn” khác nhau, từ đó chọn lọc “góc nhìn” cực tốt để vẽ hình. Các bước này thường khiến chút khó khăn cho học sinh trong thời hạn đầu new tiếp cận bộ môn HHKG, mặc dù nhiên chỉ việc sau một thời hạn luyện tập các em sẽ dần dần hình thành tư duy trừu tượng, tài năng tưởng tượng hình không khí và sẽ dễ dàng tìm được “góc nhìn” xuất sắc nhất, tức là cách vẽ hình tốt nhất ngay sau khoản thời gian đọc đề bài.
2.3.2. Xây đắp các bài bác tập về tiết diện trong “§3. Đường thẳng tuy vậy song với phương diện phẳng với §4. Nhì mặt phẳng tuy nhiên song”
sau khi học song “§1. Đại cưng cửng về mặt đường thẳng với mặt phẳng” với được thực hành giải những bài tập như trên, tôi phân biệt ở các em đã và đang hình thành năng lực tư duy trong môn Hình học; kĩ năng biểu diễn hình học, kỹ năng giám sát của học tập sinh văn minh rất nhiều, những em rất thích thú khi đứng trước một việc về dựng với tính diện tích s của thiết diện. Đây là đại lý rất đặc biệt quan trọng tạo nền tảng bền vững và kiên cố về kiến thức và kỹ năng hình học không khí cho học viên khi tiếp cận những nội dung kiến thức cao hơn. Chính vì vậy việc thi công các bài bác tập ở vị trí này (§3. Đường thẳng song song với phương diện phẳng và §4. Nhị mặt phẳng tuy vậy song) có chức năng tiếp tục có mặt các năng lượng tư duy, năng lực tính toán; củng cố kỹ năng và rèn luyện các kĩ năng đã tất cả ở bài học trước.
các bài tập tôi kiến tạo vẫn triệu tập vào việc dựng và tính diện tích s của thiết diện khi thiết diện là các hình tam giác, tứ giác, ngũ giác cùng với độ phức hợp được nâng dần lên.
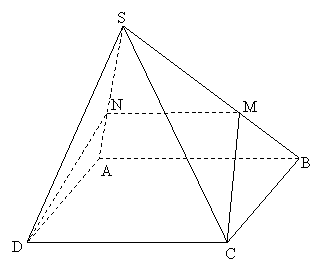
Bài 2.1. đến hình chóp S.ABCD có đáy là hình vuông vắn cạnh , các ở kề bên bằng nhau và bằng
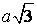
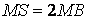
a) xác định thiết diện của hình chóp với khía cạnh phẳng (P).
b) Hãy tính diện tích thiết diện theo .
| Phân tích: (Hình 2.1) - tiết diện là hình thang cân MNDC. - Tính được những cạnh:
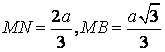 - áp dụng định lí Côsin vào tam giác SBC tính được:
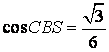 - liên tục sử dụng định lí Côsin vào tam giác BCM tính được 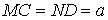 - Từ kia tính được:
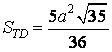 |
 |
Nhận xét 2.1:
1. Bài bác tập này có thiết kế dựa trên bài tập trong SGK với việc bổ sung cập nhật thêm những giả thiết về các cạnh của hình chóp với yêu ước tính diện tích thiết diện. Câu hỏi tính diện tích sẽ dễ dãi hơn nếu mang lại M là trung điểm của SB, vì lúc ấy học sinh chỉ cần sử dụng phương pháp tính độ dài mặt đường trung tuyến đường trong tam giác SBC là tính được CM.
2. Việc thay đổi linh hoạt trả thiết của việc (chẳng hạn như vị trí của điểm M ở bài 2.1) là 1 cách buộc học sinh phải tư duy tra cứu cách giải quyết và xử lý khác khi trả thiết của vấn đề đã chuyển đổi và cách giải quyết và xử lý cũ không hề phù hợp. Từ bỏ đó có mặt và tập luyện cho học sinh khả năng tứ duy linh hoạt, không theo lối mòn.
Dưới đây là một số bài bác tập của phần này nhưng mà tôi đã thiết kế và tổ chức dạy học ở đơn vị công tác:
Bài 2.2.
Xem thêm: 65 mẫu vách ngăn giữa phòng khách và cầu thang dạng cột đẹp và sang trọng
cho hình chóp S.ABCD có đáy là hình vuông vắn cạnh , các bên cạnh bằng nhau và cùng bằng . Gọi M là một trong những điểm trên cạnh SA làm thế nào để cho
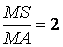
a) xác định thiết diện của hình chóp với mặt phẳng (P).
b) Hãy tính diện tích s thiết diện theo .
Phân tích: (Hình 2.2)
| Hình 2.2 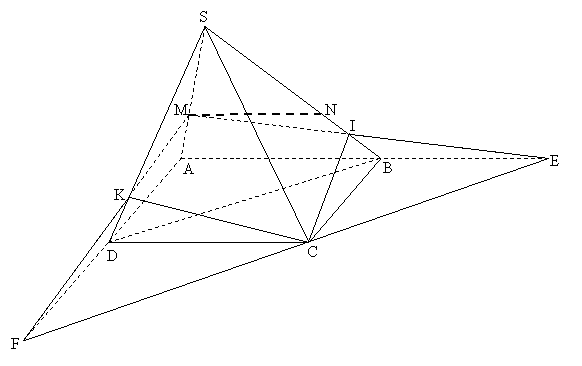 |
- tiết diện là tứ giác MKCI (Ở Hình 2.2: EF//BD)
- rất có thể định phía cho học viên tính diện tích thiết diện theo các cách như bài xích 1.2. Thế thể:
Cách 1:
- Tính diện tích của tam giác MEF:
+ bằng cách sử dụng định lí Côsin cho những tam giác MAE, MAF tính được
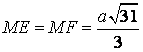
+ Áp dụng đặc thù đường trung bình trong
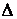
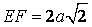
+ Từ đó tính được
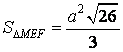
- Tiếp theo, ta cần xác minh xem những điểm I cùng K khớp ứng chia những đoạn ME và MF theo tỉ số là bao nhiêu?
+ có nhiều cách để giải quyết sự việc này, chẳng hạn, tự M ta kẻ con đường thẳng song song với AB, cắt SB tại N thì có thể thấy ngay:
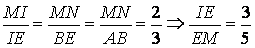
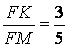
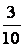
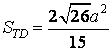
cách 2:
- Chia việc tính diện tích thiết diện thành vấn đề tính diện tích hai tam giác MIC với MKC. để ý rằng do đặc điểm đối xứng đề xuất hai tam giác này bằng nhau.
- Tính độ lâu năm 3 cạnh của tam giác MIC theo định lí Côsin và kế tiếp áp dụng cách làm Hêrông rất có thể tính được diện tích s tam giác này.
Bài 2.3. Cho hình chóp S.ABC có đáy là tam giác phần đa cạnh , cạnh
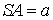
a) xác định thiết diện của hình chóp với khía cạnh phẳng (P)
b) Tính diện tích s của tiết diện theo .
Phân tích: (Hình 2.3)
| - thiết diện là hình thang MNPQ - Để tính diện tích thiết diện, ta rất có thể "lạm dụng" một đặc thù về mặt đường thẳng vuông góc với mặt phẳng ở Chương III: tình dục vuông góc, từ đó suy ra PQ với MN là những đường thẳng vuông góc cùng với (ABC), dẫn đến tứ giác MNPQ là hình thang vuông tại phường và N. - Tính được 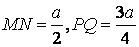 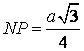 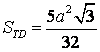 |
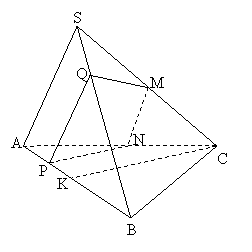 |
Nhận xét 2.2: Việc "lạm dụng" đặc thù ở về mặt đường thẳng vuông góc với khía cạnh phẳng ngơi nghỉ Chương III: quan hệ nam nữ vuông góc khi giải quyết và xử lý bài toán này là hòa hợp lí, bởi nó làm cho lời giải trở đề nghị gọn gàng, mạch lạc. Không chỉ có vậy việc "lạm dụng" này sẽ không làm cho học viên cảm thấy trở ngại bởi ở chương trình hình học tập lớp 9 những em cũng đã những bước đầu tiên làm quen thuộc với có mang "Đường trực tiếp vuông góc với mặt phẳng".
Bài 2.4. Cho hình chóp S.ABCD có toàn bộ các cạnh bởi . Gọi O là giao điểm của AC với BD, I là trung điểm của OC, (P) là phương diện phẳng trải qua I và tuy vậy song với hai tuyến đường thẳng BD, SC.
a) xác minh thiết diện của hình chóp với khía cạnh phẳng (P)
b) Tính diện tích của thiết diện theo .
Phân tích: (Hình 2.4)
| - tiết diện là ngũ giác NPQKM. - có thể chỉ ra cho học viên thấy từ đặc điểm 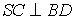
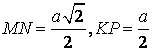 nên có diện tích
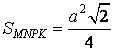 |
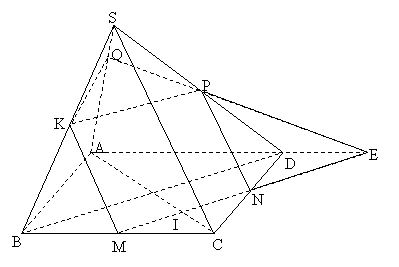 |
- Tam giác QKP cân tại Q, có:
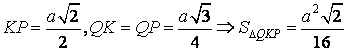
- Từ đó suy ra được
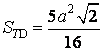
Nhận xét 2.3: Có thể hướng dẫn học viên tính diện tích ngũ giác MNPQK theo cách 1 của bài bác 2.2, cố thể:
- hotline F là giao của QK và EM thì sẽ chứng minh được:
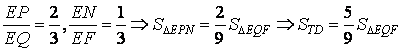
- sử dụng định lí Côsin tính được độ dài các cạnh
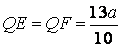

bài 2.5. Cho hình lập phương ABCD.A"B"C"D" có cạnh bởi . điện thoại tư vấn I là trọng tâm của hình vuông vắn ABCD, (P) là phương diện phẳng trải qua I và song song với hai tuyến phố thẳng BD" cùng B"C.
a) khẳng định thiết diện của hình lập phương với mặt phẳng (P).
b) Tính diện tích của tiết diện theo .
Phân tích: (Hình 2.5)
| - Để dựng thiết diện, chỉ cần dựng đường thẳng qua I, song song với BD" giảm DD" tại p. . Khi đó p là trung điểm của DD". Kế tiếp dựng mặt đường thẳng qua P tuy vậy song cùng với A"D cắt A"D" trên trung điểm Q. Trường đoản cú đó khẳng định được thiết diện là ngũ giác MNPQK. - Để tính diện tích thiết diện, ta rất có thể hướng dẫn học sinh tính tương tự như theo giải pháp của bài xích 1.3, từ đó tính được --> |