Những bài tập hằng đẳng thức nâng cao được tổng phù hợp dưới bài viết sẽ giúp chúng ta học sinh luyện tập các dạng bài xích tập liên quan đến solo thức với đa thức cùng phép nhân nhiều thức với đa thức. Thông qua đó giúp các em học sinh ôn tập, củng nạm và rèn luyện thêm kiến thức đã học tập trong chương trình Toán 8!
Một số bài tập về hằng đẳng thức nâng cao
Bài 1: sử dụng 7 hằng đẳng thức Viết các biểu thức sau dưới dạng tổng
(2x + 1)²
(2x + 3y)²
(x + 1)(x – 1)
m² – n²
(5x + 3yz)²
(yx – 3ab)²
(x² + 3)(xˆ4 + 9 – 3x²)
(9x + 3)²
(xy + 2yz)²
Lời giải
(2x+1)² = 4x²+ 4x +1
(2x+3y)² = 4x² + 2.2x.3y + 9y² = 4x² + 12x.y + 9y²
(x+1)(x-1) = x²-1
m² – n² = (m – n)(m + n)
(5x+3yz)² = 25x² + 2.5x.3yz + 9y²z² = 25x² + 30xyz + 9y²z²
(yx – 3ab)² = y²z² – 2.yx.3ab + 9a²b²
(x²+3)(xˆ4 + 9 – 3x²) = (x²)² + 3³ = x>xˆ4+27
(9x+3)² = 81x² + 54x + 9
(xy+2yz)² =x²y² + 2.xy.2yz + 4y²z² = x²y² +4xy² z + 4y² z²
Hằng đẳng thức nâng cao
Bài 2: sử dụng 7 hằng đẳng thức xứng đáng nhớ với rút gọn biểu thức sau:
A=(x+y)² – (x-y)²
- cách 1: khai triển từng hằng số trong biểu thức B bởi hằng đẳng thức
(A ± B)² = A² ± 2AB+B²
A = (x+y)² – (x-y)² = x² + 2xy + y² – (x² – 2xy + y²) = 4xy
- giải pháp 2: thực hiện hằng đẳng thức A²–B = (A + B)(A – B)
A=(x+y)² – (x-y)² = (x+y+x-y)(x+y-x+y) = 2x.2y = 4xy
B = (x+y)² – 2(x+y)(x-y) + (x-y)²
- bí quyết 1: triển khai từng hằng số vào biểu thức B bởi hằng đẳng thức
(A ± B)² = A² ± 2AB+B²
B = (x+y)² – 2(x+y)(x-y) + (x-y)² = x² + 2xy + y² – 2x² + 2y² + x² – 2xy + y² = 4y²
- phương pháp 2:
B = (x+y)² – 2(x+y)(x-y) + (x-y)² = (x + y – x + y)² = (2y)² = 4y²
Bài 3: Tính nhanh những biểu thức sau
153² + 94.153 + 47²
126² – 126.152 + 5776
Lời giải:
153² + 94.153 + 47² = 153² + 2.47.153 + 47² = (153+47)² = 200² = 40000
126² – 126.152 + 5776 = 126² – 2.126.76 + 76² = (126-76)² = 50²
Bài 4: Tính:
a, (x + 2y)2
b, (x – 3y)(x + 3y)
c, (5 – x)2
Lời giải:
a, (x + 2y)2 = x2 + 4xy + 4y2
b, (x – 3y)(x + 3y) = x2 – (3y)2 = x2 – 9y2
c, (5 – x)2 = 52 – 10x + x2 = 25 – 10x + x2
Bài 5: Tính:
a, (x – 1)2
b, (3 – y)2
c, (x – 1/2)2
Lời giải:
a, (x – 1)2 = x2 –2x + 1
b, (3 – y)2 = 9 – 6y + y2
c, (x – 1/2)2 = x2 – x + 1/4
Bài tập hằng đẳng thức
Bài 6: Viết những biểu thức sau bên dưới dạng bình phương một tổng:
a, x2 + 6x + 9
b, x2 + x + 1/4
c,2xy2 + x2y4 + 1
Lời giải:
a, x2 + 6x + 9 = x2 + 2.x.3 + 32 = (x + 3)2
b, x2 + x + 1/4 = x2 + 2.x.1/2 + (1/2 )2 = (x + 1/2)2
c, 2xy2 + x2y4 + 1 = (xy2)2 + 2.xy2.1 + 12 = (xy2 + 1)2
Bài 7: Rút gọn biểu thức:
a, (x + y)2 + (x – y)2
b, 2(x – y)(x + y) + (x + y)2 + (x – y)2
c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)
Lời giải:
a, (x + y)2 + (x – y)2
= x2 + 2xy + y2 + x2 – 2xy + y2
= 2x2 + 2y2
b, 2(x – y)(x + y) + (x + y)2 + (x – y)2
= <(x + y) + (x – y)>2 = (2x)2 = 4x2
c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)
= (x – y + z)2 + 2(x – y + z)(y – z) + (y – z)2
= <(x – y + z) + (y – z)>2 = x2
Bài 8: Biết số tự nhiên và thoải mái a phân tách cho 5 dư 4. Chứng minh rằng a2 phân tách cho 5 dư 1.
Bạn đang xem: Các hằng đẳng thức nâng cao
Lời giải:
Số tự nhiên a phân tách cho 5 dư 4, ta có: a = 5k + 4 (k ∈N)
Ta có: a2 = (5k + 4)2
= 25k2 + 40k + 16
= 25k2 + 40k + 15 + 1
= 5(5k2 + 8k +3) +1
Ta có: 5(5k2 + 8k + 3) ⋮ 5
Vậy a2 = (5k + 4)2 chia cho 5 dư 1.
Bài 9: Tính quý hiếm của biểu thức sau:
a, x2 – y2 trên x = 87 cùng y = 13
b, x3 – 3x2 + 3x – 1 tại x = 101
c, x3 + 9x2+ 27x + 27 trên x = 97
Lời giải:
a, Ta có: x2 – y2 = (x + y)(x – y)
b, gắng x = 87, y = 13, ta được:
x2 – y2 = (x + y)(x – y)
= (87 + 13)(87 – 13)
= 100.74 = 7400
c, Ta có: x3 + 9x2 + 27x + 27
= x3 + 3.x2.3 + 3.x.32 + 33
= (x + 3)3
Thay x = 97, ta được: (x + 3)3 = (97 + 3)3 = 1003 = 1000000
Bài 10: minh chứng rằng:
a, (a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2) = 2a3
b, (a + b)<(a – b)2 + ab> = (a + b)
c, (a2 + b2)(c2 + d2) = (ac + bd)2 + (ad – bc)2
Lời giải:
a, Ta có: (a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2) = a3 + b3 + a3 – b3 = 2a3
Vế trái bằng vế phải đề xuất đẳng thức được bệnh minh.
b, Ta có: (a + b)<(a – b)2 + ab> = (a + b)
= (a + b)(a2 – 2ab + b2) = a3 + b3
Vế phải bằng vế trái yêu cầu đẳng thức được chứng minh.
c, Ta có: (ac + bd)2 + (ad – bc)2
= a2c2 + 2abcd + b2d2 + a2d2 – 2abcd + b2c2
= a2c2 + b2d2 + a2d2 + b2c2 = c2(a2 + b2) + d2(a2 + b2)
= (a2 + b2)(c2 + d2)
Vế phải bởi vế trái đề xuất đẳng thức được hội chứng minh.
Bài 11: chứng tỏ rằng:
a, x2 – 6x + 10 > 0 với tất cả x
b, 4x – x2 – 5
Lời giải:
a, Ta có: x2 – 6x + 10 = x2 – 2.x.3 + 9 + 1 = (x – 3)2 + 1
Vì (x – 3)2 ≥ 0 với đa số x bắt buộc (x – 3)2 + 1 > 0 phần đông x
Vậy x2 – 6x + 10 > 0 với đa số x.
b, Ta có: 4x – x2 – 5 = -(x2 – 4x + 4) – 1 = -(x – 2)2 -1
Vì (x – 2)2 ≥ 0 với tất cả x yêu cầu –(x – 2)2 ≤ 0 với mọi x.
Suy ra: -(x – 2)2 -1 ≤ 0 với mọi x
Vậy 4x – x2 – 5
Bài 12: Tìm giá trị nhỏ tuổi nhất của những đa thức:
a, p. = x2 – 2x + 5
b, Q = 2x2 – 6x
c, M = x2 + y2 – x + 6y + 10
Lời giải:
a, Ta có: p. = x2 – 2x + 5 = x2 – 2x + 1 + 4 = (x – 1)2 + 4
Vì (x – 1)2 ≥ 0 buộc phải (x – 1)2 + 4 ≥ 4
Suy ra: p. = 4 là giá chỉ trị nhỏ bé nhất ⇒ (x – 1)2 = 0 ⇒ x = 1
Vậy p. = 4 là giá bán trị nhỏ xíu nhất của đa thức khi x = 1.
b, Ta có: Q = 2x2 – 6x = 2(x2 – 3x) = 2(x2 – 2.3/2 x + 9/4 – 9/4 )
= 2<(x – 2/3 ) – 9/4 > = 2(x – 2/3 )2 – 9/2
Vì (x – 2/3 )2 ≥ 0 nên 2(x – 2/3 )2 ≥ 0 ⇒ 2(x – 2/3 )2 – 9/2 ≥ – 9/2
Suy ra: Q = – 9/2 là giá trị nhỏ nhất ⇒ (x – 2/3 )2 = 0 ⇒ x = 2/3
Vậy Q = – 9/2 là giá bán trị nhỏ nhất của đa thức lúc x = 2/3 .
c, Ta có: M = x2 + y2 – x + 6y + 10 = (y2 + 6y + 9) + (x2 – x + 1)
= (y + 3)2 + (x2 – 2.1/2 x + 1/4 + 3/4) = (y + 3)2 + (x – 1/2)2 + 3/4
Vì (y + 3)2 ≥ 0 và (x – 1/2)2 ≥ 0 đề nghị (y + 3)2 + (x – 1/2)2 ≥ 0
⇒ (y + 3)2 + (x – 12)2 + 3 phần tư ≥ 3/4
⇒ M = ba phần tư là giá trị nhỏ tuổi nhất khi (y + 3)2 =0
⇒ y = -3 cùng (x – 1/2)2 = 0 ⇒ x = 1/2
Vậy M = 3 phần tư là giá trị nhỏ dại nhất tại y = -3 với x = 1/2
Hy vọng rằng với mọi ví dụ và những bài tập về hằng đẳng thức trên đây đang giúp cho bạn có một kiến thức và kỹ năng nền vững vàng chãi mang lại môn Toán nói chung và phần hằng đẳng thức nói riêng.
Cùng với 7 hằng đẳng thức xứng đáng nhớ, các hằng đẳng thức mở rộng cũng rất được áp dụng các vào giải quyết các việc trong đại số tương tự như hình học. Hãy thuộc giaoducq1.edu.vn mày mò những hằng đẳng thức mở rộng, cũng giống như cách chứng tỏ nhé!
Các hằng đẳng thức mở rộng cơ bản
Hằng đẳng thức bậc 2 mở rộng lớn
((a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc)((a+b-c)^2=a^2+b^2+c^2+2ab-2ac-2bc)((a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd)Hằng đẳng thức bậc 3 mở rộng lớn
((a+b+c)^3=a^3+b^3+c^3+3(a+b)(a+c)(b+c))(a^3+b^3=(a+b)^3-3ab(a+b))(a^3-b^3=(a-b)^3+3ab(a-b))(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-bc))Hằng đẳng thức bậc 4 mở rộng
((a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4)Hằng đẳng thức bậc 5 mở rộng
((a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5)Hằng đẳng thức bậc 6 mở rộng
((a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6)Hằng đẳng thức bậc 7 mở rộng
((a+b)^7=a^7+7a^6b+21a^5b^2+35a^4b^3+35a^3b^4+21a^2b^5+7ab^6+b^7)
Các hằng đẳng thức không ngừng mở rộng nâng cao
Bình phương của (n) số hạng ((n>2))
((a_1+a_2+a_3+…+a_n-1+a_n)^2=a_1^2+a_2^2+a_3^2+…+a_n^2+2a_1a_2+2a_1a_3+…+2a_1a_n+2a_2a_3…+a_n-1a_n)Hằng đẳng thức (a^n+b^n) ( với n là số lẻ)(a^n+b^n=(a+b)(a^n-1-a^n-2b+a^n-3b^2+…+b^n-1))Hằng đẳng thức (a^n-b^n) ( với n là số lẻ)
(a^n-b^n=(a-b)(a^n-1+a^n-2b+a^n-3b^2+…+b^n-1))Hằng đẳng thức (a^n-b^n) (với n là số chẵn)
(a^n-b^n=(a-b)(a^n-1+a^n-2b+a^n-3b^2+…+b^n-1))hoặc: (=(a+b)(a^n-1-a^n-2b+a^n-3b^2+…-b^n-1))
Cách nhớ:
***Lưu ý: gặp bài toán tất cả công thức (a^n-b^n) (với n là số chẵn) hãy nhớ mang đến công thức:
(a^2-b^2=(a+b)(a-b)) (viết ((a+b)) trước )(a^2-b^2=(a-b)(a+b)) ( viết ((a-b)) trước ).Chú ý: gặp bài toán (a^n+b^n) ( cùng với n là số chẵn) hãy nhớ
(a^2+b^2) không có công thức tổng quát đổi khác thành tích. Cơ mà một vài ngôi trường hợp quan trọng có số mũ bằng 4k bao gồm thể biến hóa thành tích được.
Nhị thức Newton với tam giác Pascal
Khai triển ((A+B)) nhằm viết dưới dạng một nhiều thức cùng với lũy thừa giảm dần của A lần lượt với (n= 0;1;2;3,…)
Ta được:
((A+B)^0=1)((A+B)^1=A+1B)((A+B)^2=A^2+2AB+B^2)((A+B)^3=A^3+3A^2B++3AB^2+B^3)((A+B)^4=A^4+4A^3B+6A^2B^2+4AB^3+B^4)((A+B)^5=A^5+5A^4B+10A^3B^2+10A^2B^3+5AB^4+B^5)| (n=0) | (1) |
| (n=1) | 1 1 |
| (n=2) | 1 2 1 |
| (n=3) | 1 3 3 1 |
| (n=4) | 1 4 6 4 1 |
| (n=5) | 1 5 10 10 5 1
|
| … | … |
Tổng những số mũ của A và B trong những số hạng đều bởi n
Các thông số cách đông đảo hai đầu thì bằng nhau ( bao gồm tính đối xứng)Mỗi số của một mẫu (trừ số đầu và số cuối) đều bởi tổng của số liền trên nó cộng với số phía trái của số tức khắc trên đó
Nhờ đó, suy ra:
((A+B)^6=A^6+6A^5B+15A^4B^2+20A^3B^3+15A^2B^4+6AB^5+B^6)
Bảng những hệ số bên trên gọi là Tam giác Pascal (nhà toán học Pascal (1623-1662)).
Xem thêm: Công Thức Hóa Học Của Khí Nitơ Là, Ứng Dụng Và Hình Thức Cung Cấp Khí Nitrogen
Nhà bác bỏ học lỗi lạc Newton (1643-1727) đã đưa ra công thức tổng thể sau:
((A+B)^n=A^n+n
A^n-1B+fracn(n-1)1.2A^n-2B^2+fracn(n-1)(n-2)1.2.3A^n-3B^3+…+fracn(n-1)1.2A^2B^n-2+n
AB^n-1+B^n)
Chứng minh hằng đẳng thức mở rộng
Dưới đó là cách chứng minh hằng đẳng thức mở rộng dễ dàng và cấp tốc nhất.
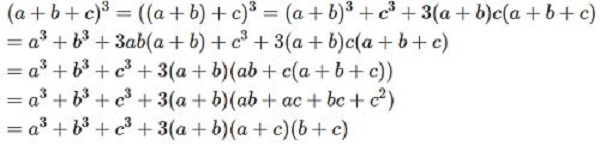
Trên đấy là kiến thức tổng phù hợp về hằng đẳng thức cơ bạn dạng và nâng cao với kiến thức mở rộng, hy vọng hỗ trợ cho chúng ta những kỹ năng và kiến thức hữu ích trong quy trình học tập của phiên bản thân. Trường hợp thấy bài viết chủ đề hằng đẳng thức mở rộng này thú vị, hãy nhờ rằng share lại nha những bạn! Chúc các bạn luôn học tập tốt!