Chuyên đề hình học không gian lớp 9 gồm những gì? Công thức hình học lớp 9 có thật sự khó nhớ như bạn nghĩ? Đừng quá lo lắng! Những thắc mắc này sẽ được gia sư Thành Tâm giải đáp qua bài viết dưới đây. Hình không gian tuy khó nhưng chúng có nhiều điều rất thú vị.
Bạn đang xem: Các công thức hình học lớp 9
Điều quan trọng hơn cả, khi các bạn nắm vững được kiến thức này thì sẽ có nền tảng cơ bản để học tốt hình học lớp 11. Cùng gia sư Thành Tâm tìm hiểu thôi nào!

Hình học không gian lớp 9 học những gì?
Theo nội dung chương trình sách giáo khoa lớp 9, phần hình học không gian thuộc chương 4: Hình trụ, hình nón và hình cầu. Nội dung của chương này trải dài qua 4 bài. Cụ thể:
Bài 1: Hình trụ, diện tích xung quanh và thể tích hình trụ.Bài 2: Hình nón, hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt.Bài 3: Hình cầu. Diện tích và thể tích hình cầu.Bài 4: Ôn tập chương.Sai lầm lớn nhất trong việc học công thức toán là bỏ qua vấn đề kiến thức nền tảng rồi đến gần thời điểm diễn ra các kì thi lại không biết mình học cái gì. Nghe thì có vẻ hơi vô lý nhỉ nhưng nó là “thực trạng” của phần lớn học sinh lớp 9 hiện nay.
Hình trụ – Công thức diện tích xung quanh và thể tích hình trụ
Hình trụ là hình được giới hạn bởi mặt trụ và hai đường tròn có đường kính bằng nhau.
Hình trụ tròn: Khi quay hình chữ nhật quanh một cạnh cố định, ta có một hình trụ.
Công thức tính diện tích xung quanh hình trụ: A= 2πrhCông thức tính thể tích hình trụ: V = πr²h (Thể tích hình trụ bằng diện tích đáy nhân với chiều cao).
Trong đó:
r: bán kính hình trụh: chiều cao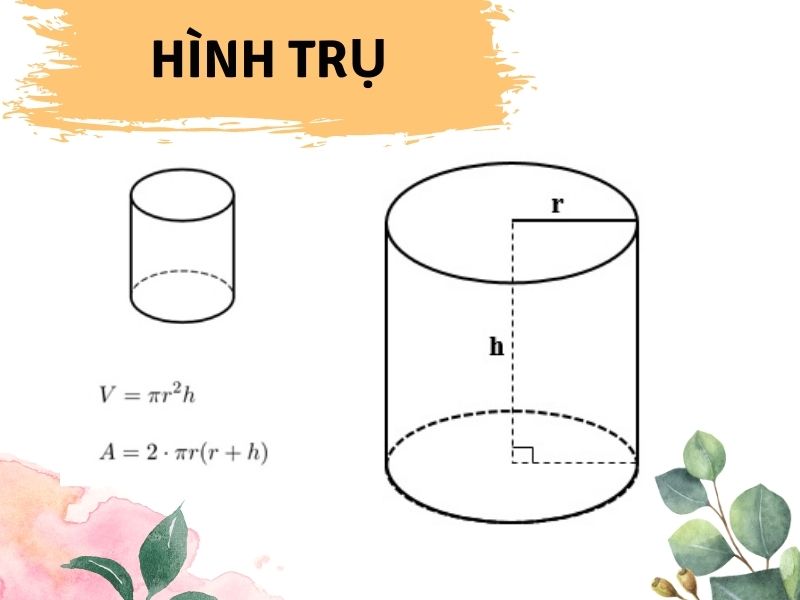
Ví dụ: Từ một tấm tôn hình chữ nhật, kích thước 50cm 189cm người ta cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50cm. Hãy tính:
a) Diện tích tôn để làm hai đáy;
b) Thể tích của hình trụ được tạo thành.
Hướng dẫn giải:
a/ Vì chiều cao của hình trụ là 50cm nên chu vi hình tròn đáy là C = 189cm.
Ta có: C= 2πR suy ra R = C/2π = 189/2π = 30 (cm)
Diện tích tôn để làm hai đáy: S = 2πR² = 2π.30² = 1800π (cm²)
b/ Thể tích hình trụ: V = πR²h = π.30². 50 = 45000π (cm³)
Công thức diện tích xung quanh và thể tích của hình nón, hình nón cụt
Hình nón là gì? Khi quay tam giác vuông AOC quanh cạnh góc vuông OA cố định thì được một hình nón.
Gọi bán kính đáy của hình nón là r, đường sinh là l, chiều cao h. Khi đó, ta có:
Hình nón:
Công thức tính diện tích xung quanh của hình nón: S = πrlCông thức tính thể tích của hình nón: V = 1/3πr²h
Hình nón cụt:
Công thức tính diện tích xung quanh của hình nón cụt: V = π(r1 + r2)lCông thức tính thể tích của hình nón cụt: V = 1/3πh((r1 + r2)² – r1.r2)
Ví dụ: Một hình nón có bán kính đáy bằng 6cm, chiều cao bằng trung bình cộng của bán kính đáy và đường sinh. Chứng minh rằng hình nón này có số đo diện tích toàn phần (tính bằng cm2) đúng bằng số đo thể tích (tính bằng cm3).

Hình cầu – Công thức diện tích xung quanh và thể tích hình cầu
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.
Khi cắt mặt cầu bán kính R bởi một mặt phẳng, ta được một đường tròn. Khi đó:
Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm gọi là đường tròn lớn.Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi quan tâm.Một hình cầu có bán kính R, ta có:
Diện tích mặt cầu: S = 4πR² hay S = πd² (d là đường kính của mặt cầu).Thể tích hình cầu: V = 4/3πR³Ví dụ: Hai hình cầu có hiệu các bán kính bằng 3cm và hiệu các thể tích bằng 1332π cm3. Tính hiệu các diện tích của hai mặt cầu.

Bài tập hình học không gian lớp 9
Bài 1: Một hình nón có mặt cắt chứa trục là một tam giác đều. Chứng minh rằng diện tích xung quanh bằng hai lần diện tích đáy.
Bài 2: Một chao đèn có dạng mặt xung quanh của một hình nón cụt. Các bán kính đáy lần lượt là R1 = 5cm; R2 = 13cm. Biết diện tích xung quanh của chao đèn là 306π cm2. Tính chiều cao của chao đèn.
Bài 3: Một đống cát hình nón có chu vi đáy là 12,56m. Người ta dùng xe cải tiến để chở đống cát đó đi 10 chuyến thì hết. Biết mỗi chuyến chở được 250 dm3. Tính chiều cao của đống cát (làm tròn đến dm).
Bài 4: Một hình trụ có diện tích toàn phần bằng 432π cm2 và chiều cao bằng 5 lần bán kính đáy. Chứng minh rằng diện tích xung quanh bằng 10 lần diện tích đáy.
Bài 5: Một bình thuỷ tinh hình trụ chứa nước. Trong bình có một vật rắn hình cầu ngập hoàn toàn trong nước. Khi người ta lấy vật rắn đó ra khỏi bình thì mực nước trong bình giảm đi 48,6mm. Biết đường kính bên trong của đáy bình là 50mm, tính bán kính của vật hình cầu.
Bài 6: Cho hình nón có đỉnh S, đường kính 2R chiều cao SH = R . Tích thể tích của hình nón
Bài 7: Một hình cầu có thể tích bằng 972π cm3. Tính diện diện tích của mặt cầu đó?
Cách nhớ các công thức hình học không gian lớp 9
Là một giáo viên đang dạy chương trình toán lớp 9, Thành Tâm hiểu được những khó khăn mà con trẻ đang gặp phải. Các công thức toán lý hóa cứ “na ná” giống nhau và lên đến hàng trăm các công thức khác nhau. Do vậy, việc nhầm lẫn giữa chúng là điều bình thường.
Đến đây sẽ có nhiều bạn thắc mắc rằng: Vậy có bí kíp nào để ghi nhớ các công thức hình học không gian lớp 9 một cách chính xác và nhanh nhất không? Câu trả lời đó là KHÔNG, cho đến nay vẫn không có câu thần chú để “giải cứu” các công thức toán này cả. Sự thật lúc nào cũng phũ phàng nhỉ!
Do vậy, điều quan trọng nhất để giúp các bạn ghi nhớ đó chính là ghi chép và vận dụng chúng để làm bài tập mà thôi. Bên cạnh đó, mỗi bạn sẽ tự đúc kết được kinh nghiệm học tập môn hình học không gian của riêng mình trong quá trình làm bài. Điều này tùy thuộc vào kĩ năng và tư duy các của bạn nhé!
Suy cho cùng, cách học giỏi toán phần hình học lớp 9 hay bất kì phần nào cũng vậy, các em phải:
Nắm chắc kiến thức ở sách giáo khoa.Không nhồi nhắt công thức hay bài tập quá nhiều.Lắng nghe thầy cô giáo giảng bài.Không hiểu thì phải hỏi, hỏi để được thầy cô giải đáp.Tự học là yếu tố quyết định nên việc ghi nhớ công thức.TÓM LẠI LÀ:
Gia sư toán lớp 9 của Thành Tâm hi vọng qua bài viết này các bạn sẽ tóm tắt tổng hợp được các công thức hình học không gian lớp 9 một cách logic nhất. Suy cho cùng để ghi nhớ được công thức toán thì chỉ có ghi chép và làm bài tập thật nhiều mà thôi. Không có “bí kíp thần thánh” nào cả! Ngoài ra, chúng tôi cũng gửi đến các bạn một số bài tập về hình trụ, hình cầu và hình nón. Các bạn có thể tham khảo và luyện tập thêm.
Chúc các bạn thành công!
Mọi sự thắc mắc vui lòng liên hệ theo số hotline hoặc fanpage của chúng tôi để được giải đáp.
Trung tâm gia sư Thành Tâm mang đến chất lượng dịch vụ gia sư tốt nhất, chắp cánh cùng các tài năng Việt.
Công thức toán 9 là nội dung quan trọng các em cần phải nắm chắc. Bởi đây chính là căn cứ để chúng ta giải các bài tập chi tiết và chính xác nhất. Muốn hiểu thêm về điều này mời độc giả dành thời gian đọc ngay bài viết dưới đây.







Trong một tam giác vuông ta có:
Cạnh góc vuông = cạnh huyền nhân với sin góc đối = cạnh huyền nhân với cosin góc kề.Cạnh góc vuông = cạnh góc vuông còn lại nhân với tan góc đối = cạnh góc vuông còn lại nhân với cot góc kề.Trong một tam giác vuông khi cho trước hai yếu tố ta sẽ tìm được các yếu tố còn lại.Các dạng toán thường gặp hệ thức về cạnh và góc trong tam giác vuông:
Ngoài việc ghi nhớ công thức toán 9 phần Hình học các em cần nắm chắc các dạng toán thường gặp. Đối với mỗi bài tập sẽ có cách giải cũng như phương pháp riêng. Cụ thể như sau:
Dạng toán 1: Yêu cầu giải tam giác vuông
Đối với dạng bài tập này các em cần đọc kỹ yêu cầu, nắm bắt các dữ kiện đã cho. Đồng thời, chúng ta nhanh chóng áp dụng ngay các phương pháp sau:
Muốn giải tam giác ta cần tính độ dài các cạnh và số đo các góc căn cứ vào dữ kiện cho trước của bài toán.Trong một tam giác vuông ta sử dụng công thức toán 9 về hệ thức giữa cạnh và các góc của một tam giác vuông để tính toán.Các bài toán yêu cầu giải tam giác vuông bao gồm: Giải tam giác vuông khi biết rõ độ dài hai cạnh và giải tam giác vuông khi ta biết độ dài một cạnh và số đo của góc nhọn.Xem thêm: Các công thức tính nhanh hóa học hữu cơ 11 giúp giải nhanh toán hiđrocabon
Dạng toán 2: Yêu cầu tính cạnh và góc của tam giác
Để giải dạng bài tập này, các em hãy thực hiện kẻ thêm đường cao nhằm làm xuất hiện tam giác vuông. Tiếp đến chúng ta áp dụng công thức toán 9 về hệ thức giữa cạnh và góc thích hợp.
Như vậy, tổng hợp công thức toán 9 đã được trình bày chi tiết trên đây. Hi vọng các em đã tìm thấy nội dung hữu ích và vận dụng giải tốt các bài tập nhanh chóng, chính xác nhất. Các bạn học sinh hãy tìm đọc các bài viết khác tại Kiến Guru để cùng tổng hợp kiến thức và giải bài tập các môn học khác nhé!